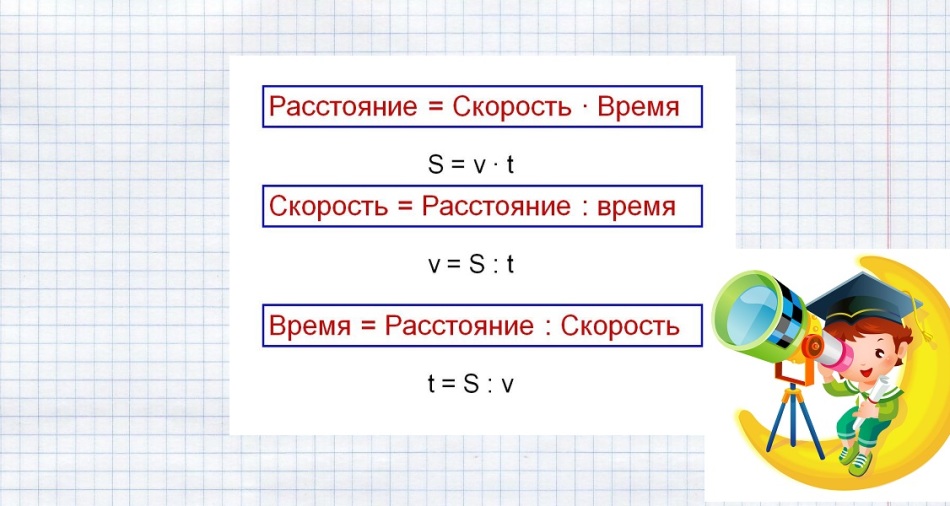
معادلة الوقت والسرعة والمسافة: الصف الرابع. كيف تجد الوقت ومعرفة السرعة والمسافة؟ كيف تجد السرعة إذا كان الوقت والمسافة معروفين؟ كيف تجد المسافة إذا كان الوقت والسرعة معروفين؟ رسم بياني لاعتماد سرعة الجسم على الوقت

كيف تحل مشاكل الحركة؟ معادلة العلاقة بين السرعة والوقت والمسافة. المهام والحلول.

معادلة الاعتماد على الوقت والسرعة والمسافة للصف الرابع: كيف يتم الإشارة إلى السرعة والوقت والمسافة؟

يمكن للناس أو الحيوانات أو الآلات التحرك بسرعة معينة. يمكنهم الذهاب بطريقة معينة في وقت معين. على سبيل المثال: اليوم يمكنك الوصول إلى مدرستك في نصف ساعة. أنت تمشي بسرعة معينة وتغطي 1000 متر في 30 دقيقة. في الرياضيات ، يُشار إلى المسار الذي يتم تجاوزه بالحرفS. يشار إلى السرعة بالحرف ت. والوقت الذي يتم فيه تغطية المسار يُرمز إليه بالحرف t.

• المسار -S
• السرعة - v
• الوقت -t

إذا تأخرت عن المدرسة ، فأنت يمكنك أن تسير على نفس المنوال في 20 دقيقة ، مما يزيد من سرعتك. هذا يعني أنه يمكن تغطية نفس المسار في أوقات مختلفة وبسرعات مختلفة.

كيف يعتمد وقت السفر على السرعة؟

كلما زادت السرعة ، زادت سرعة قطع المسافة. وكلما انخفضت السرعة ، زادت المدة التي ستستغرقها لإكمال الرحلة.

​​

كيف تجد الوقت لمعرفة السرعة والمسافة؟

لإيجاد الوقت المستغرق لقطع مسافة ، عليك معرفة المسافة والسرعة. إذا قسمت المسافة على السرعة ، فستعرف الوقت. مثال على هذه المهمة:

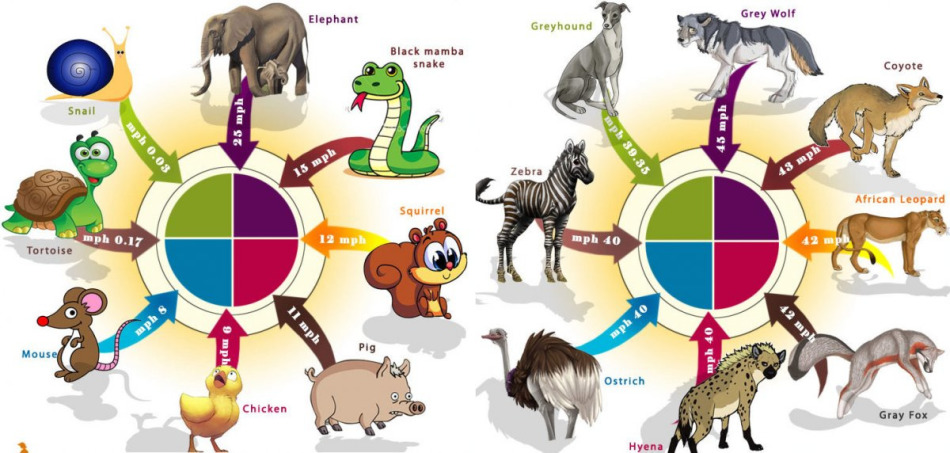
المهمة المتعلقة بالأرنب. ركض الأرنب بعيدًا عن الذئب بسرعة كيلومتر واحد في الدقيقة.ركض 3 كيلومترات إلى الحفرة. بعد فترة ، هل ركض الأرنب إلى الحفرة؟

ما مدى سهولة حل مشاكل الحركة حيث تحتاج إلى إيجاد المسافة أو الوقت أو السرعة؟

1. اقرأ المشكلة بعناية وحدد ما هو معروف من حالة المشكلة.
2. اكتب هذه البيانات على المسودة.
3. اكتب أيضًا ما هو غير معروف وما يمكن العثور عليه
4. استخدم معادلة مسائل المسافة والوقت والسرعة
5. أدخل البيانات المعروفة في الصيغة وحل المشكلة

حل لمشكلة الأرنب والذئب.

• من حالة المشكلة ، نحدد أننا نعرف السرعة والمسافة.
• نحدد أيضًا من حالة المشكلة أننا بحاجة إلى إيجاد الوقت الذي استغرقته الأرنب للركض إلى الحفرة.

نكتب هذه البيانات في مسودة على سبيل المثال:

المسافة إلى الحفرة - 3 كيلومترات

سرعة الأرنب - كيلومتر واحد في دقيقة واحدة

الوقت غير معروف

الآن لنكتب نفس الشيء في الرموز الرياضية:

)

جنوبًا- 3 كيلومترات

الخامس - 1 كم / دقيقة

ر-؟

نتذكر ونكتب صيغة إيجاد الوقت في دفتر ملاحظات:

t = S: v

الآن نكتب حل المشكلة بالأرقام:

t = 3: 1 = 3 دقائق

كيف يمكن إيجاد السرعة إذا كان الوقت والمسافة معروفين؟

لإيجاد السرعة ، إذا كان الوقت والمسافة معروفين ، يجب تقسيم المسافة على الوقت. مثال على هذه المهمة:

ركض الأرنب بعيدًا عن الذئب وركض 3 كيلومترات إلى جحره. قطع هذه المسافة في 3 دقائق. ما مدى سرعة الجري هير؟

حل مشكلة الحركة:

1. نكتب في المسودة أننا نعرف المسافة والوقت.
2. من حالة المسألة ، نحدد أننا بحاجة لإيجاد السرعة
3. نتذكر صيغة إيجاد السرعة.

معادلات لحل مثل هذه المشاكل موضحة في الصورة أدناه.

استبدل البيانات المعروفة وحل المشكلة:

المسافة إلى الحفرة هي 3 كيلومترات

كان الوقت الذي استغرقه هير للوصول إلى الحفرة 3 دقائق

السرعة غير معروفة

لنكتب هذه البيانات المعروفة بالرموز الرياضية

س- 3 كيلومترات

طن- 3 دقائق

v -؟

نكتب صيغة لإيجاد السرعة

v = S: t

نكتب الآن حل المشكلة بالأرقام:

v = 3: 3 = 1 km / min[139)]

كيفية إيجاد المسافة إذا كان الوقت والسرعة معروفة؟

لإيجاد المسافة ، إذا كان الوقت والسرعة معروفين ، اضرب في السرعة. مثال على هذه المهمة:

ركض الأرنب بعيدًا عن الذئب بسرعة كيلومتر واحد في دقيقة واحدة. استغرق الأمر ثلاث دقائق للركض إلى الحفرة. إلى أي مدى ركض هير؟

حل المشكلة: نكتب في المسودة ما نعرفه من حالة المشكلة:

سرعة الأرنب 1 كيلومتر في دقيقة واحدة

الوقت الذي ركض فيه الأرنب إلى الحفرة - 3 دقائق

المسافة - غير معروف

الآن ، دعنا نكتب نفس الشيء في الرموز الرياضية:

v - 1 كم / دقيقة

t- 3 دقائق

S -؟

نتذكر صيغة إيجاد المسافة:

S = v ⋅ t

نكتب الآن حل المشكلة بالأرقام:

S = 3 ⋅ 1 = 3 كم

كيف تتعلم حل المهام الأكثر تعقيدًا؟

لتعلم كيفية حل المهام الأكثر تعقيدًا ، تحتاج إلى فهم كيفية حل المهام البسيطة ، وتذكر العلامات التي تشير إلى المسافة والسرعة والوقت. إذا كنت لا تستطيع تذكر الصيغ الرياضية ، فيجب عليك كتابتها على قطعة من الورق والاحتفاظ بها دائمًا في متناول اليد عند حل المشكلات. قم بحل المهام البسيطة مع طفلك التي يمكنك القيام بها أثناء التنقل ، على سبيل المثال ، أثناء المشي.

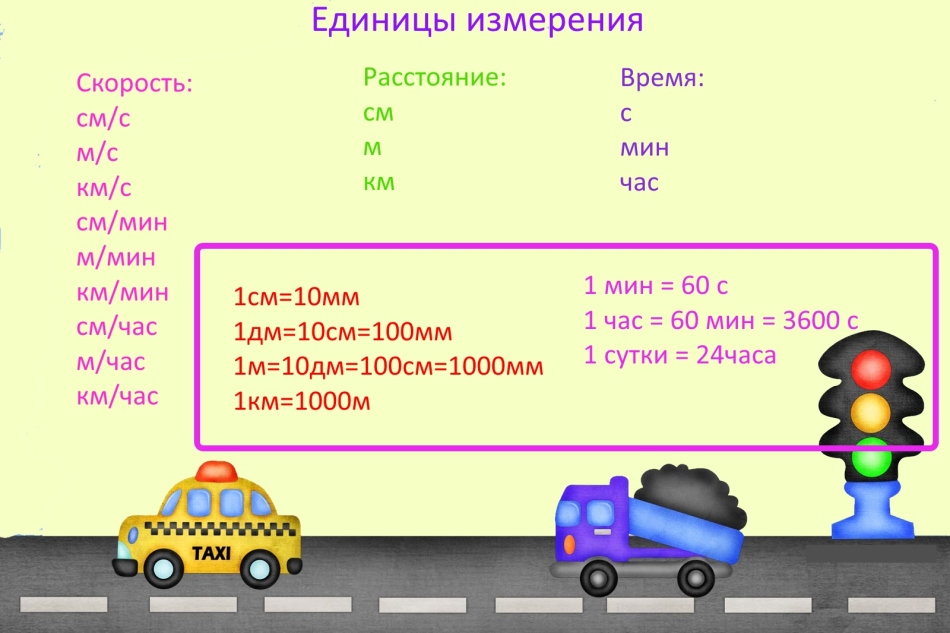
وحدات القياس

عند حل المسائل المتعلقة بالسرعة والوقت والمسافة ، غالبًا ما يخطئون لأنهم ينسون تحويل وحدات القياس.

هام: يمكن أن تكون وحدات القياس أي وحدة ، ولكن إذا كانت هناك وحدات قياس مختلفة في نفس المشكلة ، فقم بتحويلها إلى نفس وحدات القياس. على سبيل المثال ، إذا تم قياس السرعة بالكيلومترات في الدقيقة ، فيجب تمثيل المسافة بالكيلومترات ، والوقت بالدقائق.

للفضوليين [192)]: يُطلق على نظام القياس المقبول عمومًا اسم متري ، ولكن لم يكن هذا هو الحال دائمًا ، وفي روسيا القديمة ، تم استخدام وحدات قياس أخرى.

مشكلة بوا : قام الفيل الرضيع والقرد بقياس طول أفعى في خطوات. تحركوا تجاه بعضهم البعض. كانت سرعة القرد 60 سم في ثانية واحدة ، وسرعة الفيل الصغير 20 سم في ثانية واحدة. أمضوا 5 ثوان في القياس. ما هو طول البواء؟ (الحل تحت الصورة)

العلامة & lt؛ & GT. الحل:

من حالة المشكلة ، نحدد أننا نعرف سرعة القرد والفيل الصغير والوقت اللازم لقياس طول الأفعى.

لنكتب هذه البيانات:

سرعة القرد 60 سم / ثانية

سرعة الفيل الرضيع 20 سم / ثانية

الوقت - 5 ثوان

مسافة غير معروفة

لنكتب هذه البيانات برموز رياضية:

v1 - 60 سم / ثانية

v2 - 20 سم / ثانية

t - 5 ثوان

ق -؟

لنكتب صيغة المسافة ، إذا كانت السرعة والوقت معروفين:

S = v ⋅ t

دعونا نحسب المسافة التي قطعها القرد:

S1 = 60 ⋅ 5 = 300 سم [232)]

الآن دعونا نحسب المسافة التي قطعها الفيل الصغير:

S2 = 20 ⋅ 5 = 100 سم

نلخص المسافة التي قطعها القرد والمسافة التي قطعها الفيل الصغير:

S = S1 + S2 = 300 + 100 = 400 سم

رسم بياني لاعتماد سرعة الجسم على الوقت: الصورة

المسافة مغطاة بسرعات مختلفة في أوقات مختلفة.كلما زادت السرعة ، قل الوقت المستغرق للتحرك.

جدول 4 فئة: السرعة والوقت والمسافة

رقم	السرعة (كم / ساعة)	الوقت (ساعة)	المسافة (كم)
1	5	2	؟
2	12	؟	12
3	60	4	؟
4	؟	3	300
5	220	؟	440

يمكنك التخيل والتوصل إلى مهام الجدول بنفسك. فيما يلي خياراتنا لشروط المهام:

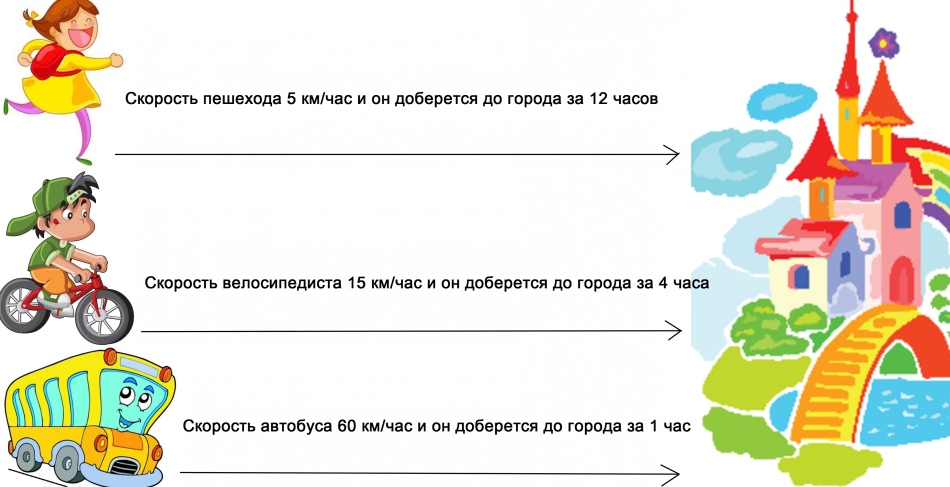
1. أرسلت أمي ذات الرداء الأحمر إلى الجدة. كانت الفتاة مشتتة باستمرار وتمشي عبر الغابة ببطء ، بسرعة 5 كم / ساعة. أمضت ساعتين في الطريق. ما المسافة التي قطعتها الرداء الأحمر خلال هذا الوقت؟
2. حمل ساعي البريد Pechkin طردًا على دراجة بسرعة 12 كم / ساعة. إنه يعلم أن المسافة بين منزله ومنزل العم فيدور هي 12 كم. ساعد Pechkin في حساب المدة التي سيستغرقها السفر؟
3. اشترى بابا كسيوشا سيارة وقرر اصطحاب العائلة إلى البحر. كانت السيارة تسير بسرعة 60 كم / ساعة وقضيت 4 ساعات على الطريق. ما المسافة بين منزل كسيوشا وساحل البحر؟
4. تجمع البط في إسفين وتوجه إلى المناطق الدافئة. رفرفت الطيور أجنحتها بلا كلل لمدة 3 ساعات وقطعت 300 كيلومتر خلال هذا الوقت. كم كانت سرعة الطيور؟
5. تحلق طائرة AN-2 بسرعة 220 كم / ساعة. أقلع من موسكو وسافر إلى نيجني نوفغورود ، والمسافة بين هاتين المدينتين 440 كم.ما هي المدة التي ستقضيها الطائرة في الطريق؟

يمكن العثور على إجابات للمشكلات المحددة في الجدول أدناه:

)

رقم	السرعة (كم / ساعة)	الوقت (ساعة)	المسافة (كم)
) 1	5	2	10
2	12	1[324)]	12
3	60	4	240
4	100	3	300
5	220	2	440

أمثلة لحل مسائل السرعة والوقت والمسافة للصف الرابع

إذا كان هناك عدة أشياء متحركة في مهمة واحدة ، فأنت بحاجة إلى تعليم الطفل أن يفكر في حركة هذه الأشياء بشكل منفصل وبعد ذلك فقط معًا. مثال على هذه المهمة:

قرر صديقان فاديك وتيما الذهاب في نزهة على الأقدام وغادرا منزليهما لمقابلة بعضهما البعض. كان فاديك يركب دراجة ، وكان تيما يمشي. كان فاديك يقود سيارته بسرعة 10 كم / ساعة ، وكان تيما يسير بسرعة 5 كم في الساعة. بعد ساعة التقيا. ما هي المسافة بين بيوت فاديك وتيما؟

يمكن حل هذه المشكلة باستخدام صيغة اعتماد المسافة على السرعة والوقت.

S = v ⋅ t

المسافة التي يقطعها فاديك على دراجة ستساوي سرعته مضروبًا بمرور الوقت في العبور.

S = 10 ⋅ 1 = 10 كيلومترات

يتم حساب المسافة التي يقطعها الموضوع بالمثل:

S = v ⋅ t

استبدل القيم الرقمية لسرعتها ووقتها في الصيغة

S = 5 ⋅ 1 = 5 كيلومترات

يجب إضافة المسافة التي قطعها فاديك إلى المسافة التي قطعها تيما.

10 + 5 = 15 كيلومترًا

كيف تتعلم حل المشكلات المعقدة التي تتطلب التفكير المنطقي؟

لتنمية التفكير المنطقي للطفل ، من الضروري حل المهام المنطقية البسيطة ثم المعقدة منها. يمكن أن تتكون هذه المهام من عدة مراحل.لا يمكنك الانتقال من مرحلة إلى أخرى إلا إذا تم حل المرحلة السابقة. مثال على هذه المهمة:

ركب أنطون دراجة بسرعة 12 كم / ساعة ، وركبت ليزا دراجة بخارية بسرعة أقل مرتين من أنطون ، ودينيس سار بسرعة أقل مرتين من سرعة ليزا. ما هي سرعة دينيس؟

لحل هذه المشكلة ، عليك أن تعرف سرعة ليزا أولاً ، وبعد ذلك فقط سرعة دينيس.

غادر اثنان من راكبي الدراجات من مدن مختلفة للقاء بعضهما البعض. كان أحدهم في عجلة من أمره وكان يركض بسرعة 12 كم / ساعة ، والثاني كان يقود على مهل بسرعة 8 كم / ساعة. المسافة بين المدن التي غادر منها راكبو الدراجات 60 كم. إلى أي مدى سيسافر كل راكب دراجة قبل أن يلتقيا؟ (حل تحت الصورة)

الحل:

• 12 + 8 = 20 (km / h) هي السرعة الإجمالية لراكبي الدراجات ، أو السرعة التي يقتربان بها من بعضهما البعض
• 60: 20 = 3 (h) هو الوقت الذي التقى فيه راكبو الدراجات
• 3 ⋅ 8 = 24 (كم) هي المسافة التي يقطعها أول راكب دراجة
• 12 ⋅ 3 = 36 (كم) تساوي المسافة التي يقطعها راكب الدراجة الثاني
• تحقق: 36 + 24 = 60 (كم) هي المسافة التي يقطعها راكبا الدراجة.
• الإجابة: 24 كم ، 36 كم.

اعرض على الأطفال حل المهام التالية على شكل لعبة. ربما يريدون أن يصنعوا مشكلتهم الخاصة حول الأصدقاء أو الحيوانات أو الطيور.

فيديو: مشاكل الحركة