معادلة حجم ومساحة السطح الكامل للكرة ، الكرة من خلال نصف قطر وقطر الكرة: القيم. أمثلة على حساب مساحة السطح وحجم الكرة ، باستخدام نصف قطر الكرة وقطرها: الوصف. كيفية العثور على حجم الكرة من خلال مساحة سطح الكرة: مثال

ستكون المقالة مفيدة لأطفال المدارس والمتقدمين المستقبليين الذين يستعدون لإجراء اختبار الدولة الموحد.

صيغة حجم الكرة عبر نصف القطر: القيمة

حجم الكرة V هو محسوبًا بالصيغة (انظر أدناه) ، حيث R هو نصف قطر الكرة ، والرقم "pi - pi ثابت رياضي ، ≈ 3.14.

هذه الصيغة أساسية!

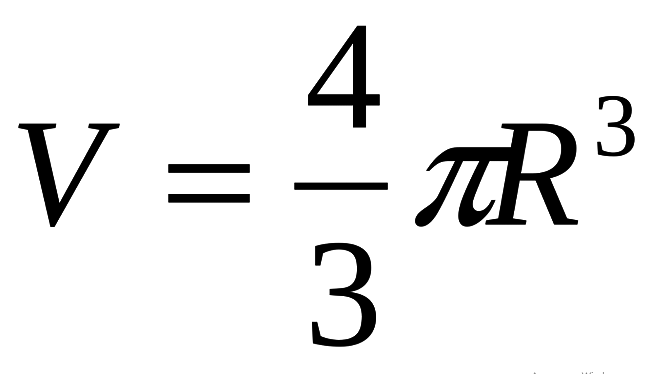
صيغة حجم الكرة من خلال القطر: القيمة

1. استخدم الصيغة الأساسية: V = 4/3 * π * R3.
2. نصف القطر R هو ½ القطر D أو R = D / 2.
3. ومن ثم: V = 4/3 * π * R3 → V = (4π / 3) * (D / 2) 3 → V = (4π / 3) * (D3 / 8) → الخامس = π د 3/6.

أو

]

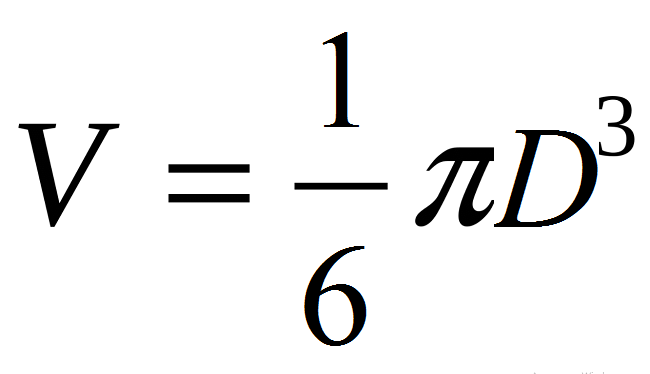
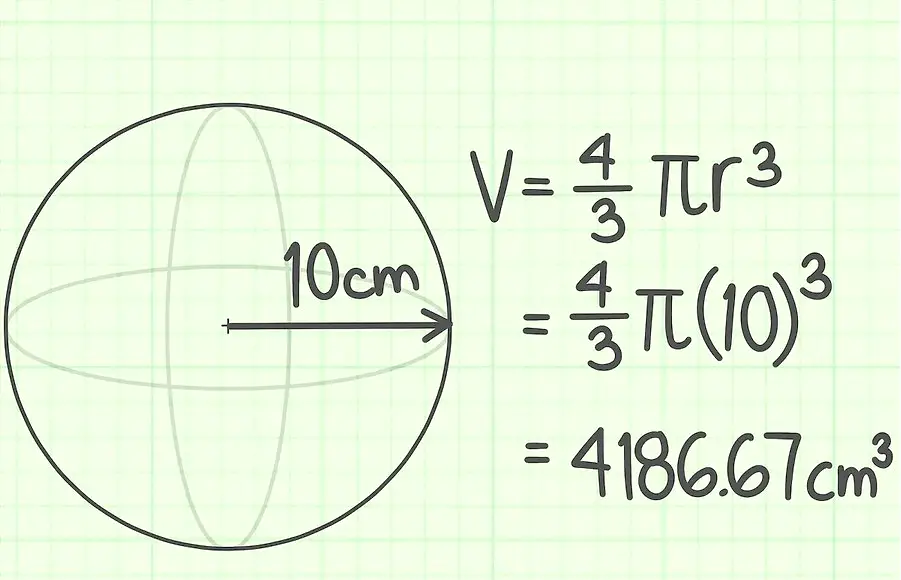
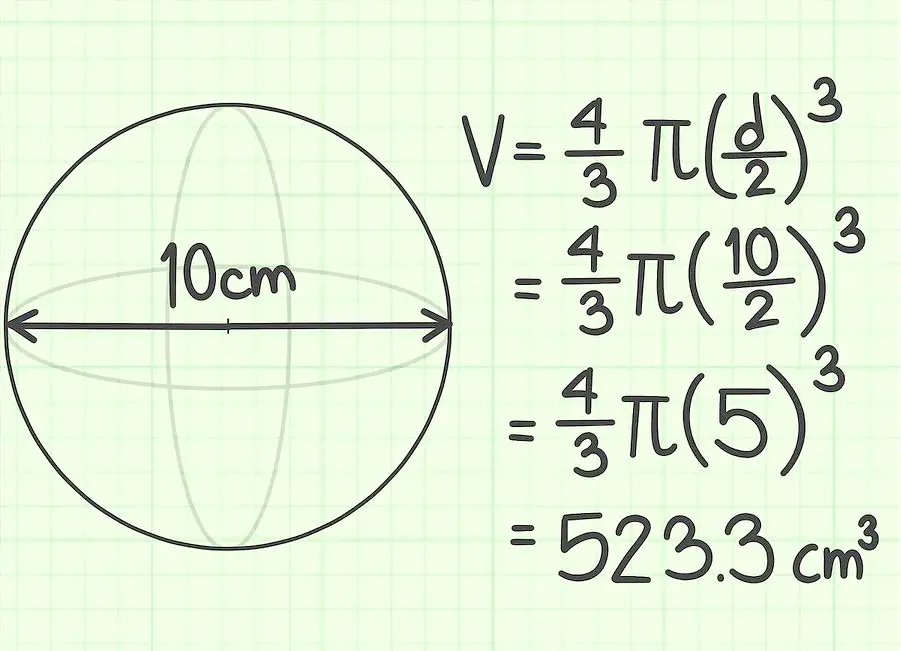
أمثلة لحساب حجم الكرة ، باستخدام نصف قطر الكرة وقطرها: الوصف

المهمة 1.

نصف قطر الكرة هو 10 انظر أوجد حجمها.

المسألة الثانية.

قطر الكرة 10 سم ، أوجد حجمها.

) المشكلة الثالثة.

نسبة قطر القمر إلى قطر الأرض هي 1: 4. كم مرة يكون حجم الأرض أكبر من حجم القمر؟

الحل:

الإجابة: 64 مرة.

هام : هناك العديد من الآلات الحاسبة عبر الإنترنت التي تتيح لك العثور بسرعة على قيمة معينة. على سبيل المثال ، خدمة Webmath.

صيغة السطح الكامل للكرة ، الكرة عبر نصف قطر: القيمة

هذه الصيغة أساسية!

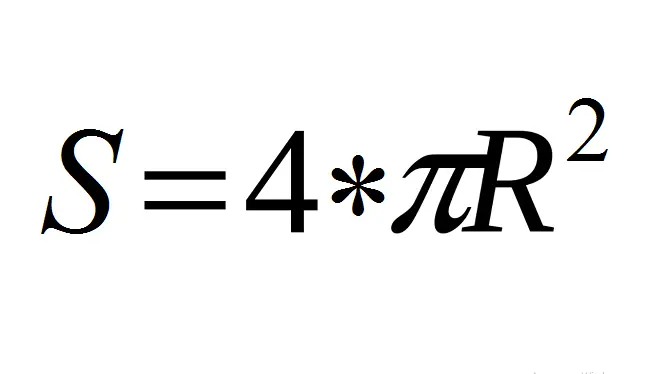
) صيغة للسطح الكلي للكرة ، الكرة من خلال القطر: القيمة

1. استخدم الصيغة الأساسية: S = 4 * π * R2.
2. نصف القطر R هو ½ القطر D أو R = D / 2.
3. ومن ثم: S = 4 * π * R2 → S = 4 * π * (D / 2) 2 → S = (4π) * (D2 / 4) → S = (4πD2) / 4 ← S = π د 2.

أو

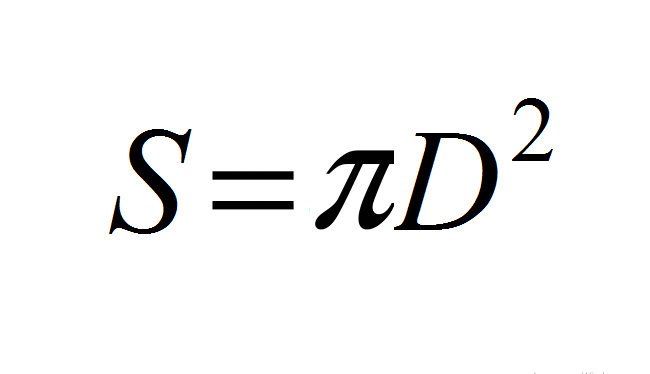
أمثلة لحساب مساحة سطح الكرة ، باستخدام نصف قطر وقطر الكرة: الوصف

المهمة 4.

المهمة 5.

المهمة 6.

كيفية العثور على حجم الكرة من خلال أسطح مساحة الكرات ، الكرات: مثال لحل مشكلة

المهمة 8.

فيديو: ЕДИ الرياضيات. حجم ومساحة أجسام الدوران.